倒立摆稳定之单节摆
一个想法
首先说一件事情啊,我有个想法,就是专门给Wolfram做一个系列的专题,喜爱Mathematica的同学想必对Wolfram有所耳闻,但是据我所知,经常上去逛和学习的人并不多,至少国内是这样子的,嘛,英语的障碍我也不是不能理解。但是Wolfram上面有很多很棒很好玩的东西和想法,每次看都会觉得不去推广它的话实在太可惜了。【我就丧心病狂的写过一个小东西,把wolfram博客上可以下载得cdf文件和nb文件全部爬下来,所谓cdf,里面内容就是原文博客以及里面的代码,所以看那个文件比看博客本身强太多了。。】
所以我就想做一个这样的专题,idea来自wolfram,说是翻译也可以,但是不是单纯的翻译,有点类似于自己看一遍,然后把自己的理解或者学到的东西记录下来,虽然也是按照原文一样一步一步来实现功能的,但是中间会乱入一些自己的相关解释,因为我本来在这里写博客就是专门写那些科普性质的东西的,而单纯完全翻译wolfram上的东西是实现不了科普的,所以,不知道这个东西有多少人感兴趣?!
Stabilized Inverted Pendulum
想法先说这么多;这次的就是来源于wolfram上的一个系列博文,说是系列,其实也就两篇,就是稳定倒立摆问题,原文叫《Stabilized Inverted Pendulum》,两篇,一篇讲怎么稳定单节的,一篇讲稳定多节的,本文讲的就是上面那幅图啦~倒立的单摆!
为什么选这篇,原因有几个:
第一,可以科普一下物理,因为虽然是力学问题,但是这个不是高中就能解决的力学知识,而很多人高中学了物理之后就再也没怎么碰过了,所以顺便做做科普!
第二,作为一个Mathematica的传教士【实验室有不少人被我拉进这个坑了!!】,我觉得这篇东西可以很好的展示Mathematica的强大的公式推导能力!!
第三,这里面正好会涉及到一些简单的控制原理,也是顺便科普~
第四,正好因为博客搬家了,这里可以直接展示CDF文件了,而这篇东西正好因为有很多需要cdf才可以很好展示的东西!!
第五,这篇东西原文本身真的很有意思啊!!
以上!!
力学分析
首先,先让我把上面的图再贴一遍吧:
对于这样一个系统,一个棍摆放置在一个小木盒上面,小木盒放在x轴上,中心距离原点距离为x,然后我们这个问题就是怎么对这个小木盒施加力f,使得上面的倒立摆可以垂直地稳定在上面!
上图可以看到倒立摆的几个参数,长度\(d\),质量\(m\),与\(x\)轴夹角\(\theta\),那么描述这个倒立摆的质心就可以用下面公式:
\(p=(\dfrac{1}{2}d \cos (\theta (t))+x(t),\dfrac{1}{2}d \sin (\theta (t)))\)
然后显然的,速度\(v\)就是位移\(p\)的导数,而动能就是\(\dfrac{1}{2}mv^2\),虽然很简单,但是还是展示一下Mathematica怎么做吧:
Mathematica Code
拉格朗日量 Lagrangian
继续下面的推导之前,有必要说一下这个,因为很多人物理的巅峰水准就是学到了大物为止,所以不一定会对拉格朗日量有所了解,所以这里就简单说明一下,不然接下来没法解释。。orz。。。如果对这个很了解得同学就赶紧跳过这一段吧,因为下面这段是一个巅峰也只有大学物理的人写出来的东西。。
拉格朗日量是分析力学里面的一个概念,好吧,请原谅我再花点时间来解释一下什么是分析力学;分析力学,说白了,那是一群数学家玩的物理,和我们所学的力学的区别是在思考问题的角度上的区别而已。。举个例子讲,就是他们才不管质量动量之类的是什么,比如对他们而言,一个系统中,大学物理水平的我们知道动量守恒,动能守恒,但是对他们而言,“哇,0.5乘一个常量再乘一个物体的速度的平方(好吧。。他们不一定知道速度是什么)加上0.5乘另一个常量乘另一个物体的速度的平方,这个和是守恒的,好神奇啊~”的说。。而且他们还知道一个常量乘第一个物体的速度加上另一个常量乘另一个物体的速度也是守恒的,而且!!!他们还神奇地发现,这两个常量分别是相同的!!他们会说,为了方便,我们管这个常量叫做物体的质量吧!~
有点吐槽属性,总而言之,分析力学就是这样的一个东西,他们是极度数学化的力学!我以前看朗道的分析力学书的时候,好像就是从一个惯性定理,外加这里要讲的拉格朗日量,就可以推出我们以前的各种定理和结论,以前写过一个短篇的笔记,讲的是分析力学的势能的结论。【按照我一个物理系的同学的说法就是,分析力学可以花一个小时用一个很牛逼的方法来解决一个高中习题册上本来花1分钟就可以算出来的东西。。好吧,我真不是黑。。】
那么分析力学怎么研究物体的运动的呢?我们普通人眼力,自由落体的运动方程是一个恒定加速运动,我们可以根据这个写出\(s=\dfrac{1}{2}at^2\)这一类公式,然后预测下一时刻物体的位置,速度之类的!
但是分析力学家眼里(真有这种家么喂?),他们会觉得,凭什么要是匀加速?他们的结论是啥?他们说,一切运动都是遵循动能减势能沿着时间\(t\)积分和最小的那条路径运动的,然后他们再定义动能减势能这个量叫拉格朗日量!!【为什么分析力学有存在的必要?因为我们的自由落体那种公式只能用于匀加速,但是却不能用于圆周运动,很多可以运用于弹性势能的运动公式却不能用于引力势能下的运动,但是对于分析力学而言,他们都是一样的,就是一切运动只要解一个关于拉格朗日量的方程就解决了~这就是分析力学的魅力所在~唉。。总算帮它洗白了。。】
可能有人不知道拉格朗日量,但是好歹知道最小作用量么?比如说几何光学里面为什么光要符合折射定律?因为光永远一定会沿着光程最短的路径传播。运动也一样,物体会怎么运动?他一定会沿着拉格朗日量关于时间的积分最小的那条路径运动的!!对于光学来说,光程是最小作用量,对于运动学来说,动能减势能那个量叫最小作用量【应该是吧。。如果说错了,请原谅我。。】。
那么是怎么解这个拉格朗日量的呢?抛开中间泛函的推导而言,就很简单:定义拉格朗日量\(L=T-V\),\(T\)是动能,\(V\)是势能,运动方程就是下面这个方程的解:
\(\dfrac{d}{dt}\dfrac{\partial L}{\partial x'(t)}-\dfrac{\partial L}{\partial x(t)}=0\)
如果系统有外力,那么加在公式右边即可!
好吧,实在不好意思,这个一写就写的有点长了。。。赶紧回主题吧。。其实不怎么懂也可以继续往下看。。
我们继续,上面我们算出了倒立摆的动能了,加上下面小木盒的动能,减去倒立摆的势能就是我们这个系统的拉格朗日量的(自然的,我们定义小木盒所在位置为零势面)。依旧的,我们把推导的工作交给Mathematica吧~ 接下来就是解下面这两个方程啦~
接下来就是解下面这两个方程啦~
\(\left\{\begin{array}{ll}\dfrac{d}{dt}\dfrac{\partial L}{\partial x'(t)}-\dfrac{\partial L}{\partial x(t)}=f(t)\\\dfrac{d}{dt}\dfrac{\partial L}{\partial \theta'(t)}-\dfrac{\partial L}{\partial \theta(t)}=0\end{array}\right.\)
接下来为了好看,我们先把上面这两个偏微分方程化简一下,然后,因为具有一般性,我们定义小木盒质量,倒立摆质量和倒立摆长度均为单位1!
Mathematica Code
体会到Mathematica推导公式的优越性么?【实验室某师兄就是为了图Mathematica推公式比较好用所以被我骗进了这个坑。。】
然后我们只要让Mathematica解这个方程就可以了。作为第一个实验,我们首先不对这个系统施与任何外力,也就是\(f(t)=0\);唯一需要注意的是,我们这里给木棍的初始角度赋予了\(\dfrac{\pi}{2}-0.001\),也就是一丁丁丁点倾斜角,大家懂得,不倾斜的话这个系统是不会动的!!
Mathematica Code
不过为了可视化整个过程,需要先写一个交互程序:【我想很多喜欢mathematica的同学都会很喜欢mathematica可以很方便的写出各种交互界面这种东西来吧~】,考虑到下面这个长长的函数对这片文章的核心理解并不重要,我就先缩起来了,感兴趣的可以自己展开看看。。
可视化接口函数
Mathematica Code
本来对于我写博客而言,最容易展示给大家的方法就是网页内嵌入CDF文件,但是考虑到不是所有看我博客的人都有装Mathematica的,所以我专门写了一小段程序做gif的,所以下面我都是放出两个结果演示,一个是gif的,一个在缩进里面的CDF文件,没有装Mathematica的童鞋是看不了CDF的,虽然CDF的流畅度比gif好,而且可以在上面操纵交互~
CDF演示
上面这个是在不加外力的情况的的自由情形,加外力\(f(t)\)的话,会怎么样呢?首先我们封装一个加任意外力的API函数:
Mathematica Code
然后我们增加一个外力\(f(t)=2.5(\dfrac{\pi}{2}-\theta (t))\),然后结果如下:
SimulatePendulum[2.5 (\[Pi]/2 - \[Theta][t])]
CDF演示
这里不难理解吧,就是加入一个负反馈,让角度\(\theta (t)\)维持在\(\dfrac{\pi}{2}\),其中前面的系数2.5是为了“把持住”这个倒立摆,原文中有实验系数为1的情况,由于力度不够,摆一下子就飞了。。。
就结果上而言,很不错了,至少比我们自己用手玩好多了是吧~
为了使得运动更加平滑,我们再把摆的速度考虑进去,于是力就变成\(f(t)=3(\dfrac{\pi}{2}-\theta (t))-\theta ‘(t)\),结果如下:

CDF演示
虽然更加的稳了,但是却不断右漂了,那我们要怎么样才可以把倒立摆稳定在\(x=0\)的位置呢?这个时候就是看我们Mathematica在控制方面的强大运用了。如果要完全理解,需要一些控制原理的知识,但是不要紧,不懂的话大家大概feel一下就行了~因为依样画葫芦的话还是没问题的!!
首先,我们要确定我们想要的最终的稳定状态是什么!!显然的,就是:
\(x(t)=0,x'(t)=0,\theta (t)=\dfrac{\pi}{2},\theta ‘(t)=0\)
所以我们就得到下面这个方程来描述当前状态距离“平衡点”有多远:
\(f(t)=k_1x(t)+k_2x'(t)+k_3(\theta (t)-\dfrac{\pi}{2})+k_4\theta ‘(t)\)
\(k_i\)我们这里一般叫做反馈增益。要怎么稳定到平衡点?Mathematica提供了很多控制方程的函数,wolfram里面提到可以用 StateSpaceModel函数来实现非线性的控制方程,它返回的是一个控制模型:
Mathematica Code
可能有人看不懂这个返回矩阵是什么意思?其实他是描述离开平衡点的话,上面四个参数\(x(t),x'(t),\theta (t),\theta ‘(t)\)两两之间的影响,比如说第三列,说明\(\theta (t)\)离开平衡点的话,会同时影响到\(x'(t)\)和\(\theta ‘(t)\),懂?不懂不要紧,feel一下就好~
然后我们有了系统模型,就可以用LQRegulatorGains来计算反馈增益\(k_i\):
Mathematica Code
为什么会有增益这个东西?是因为我们上面第二个参数指定的不同的量偏离平衡点所带来的“惩罚”,如果对人工智能啊,状态空间搜索,最优解计算这些问题比较了解的童鞋应该对惩罚函数这个概念不陌生,上面函数第二个参数说明了我们指定了惩罚函数为:
\(cost function = 1x(t)^2+10x'(t)^2+10\theta (t)^2+100\theta ‘(t)^2+1 f(t)^2\)
当然惩罚函数前面的系数我们写的比较随意,但是不管怎么说,他返回来的反馈增益\(k_i\)是让我们的系统在运动过程中累积的惩罚函数的和最小的值!!
就上面简单的两步计算,我们就可以得到我们的力度随着时间的变化函数了:
Mathematica Code
我们来看看结果:看吧,效果很好吧~这里附加解释一下,有人觉得一开始会不会向右漂出多了一点,其实也还好吧,但是如果真是强迫症发作,也很好办,记得我们上面函数对于\(x(t)\)的惩罚系数么?是1,最小的一个,也就是说我们指定的反馈系统中,我们表示我们不是很在意\(x(t)\)偏离平衡点多少,因为惩罚不重嘛~如果想要右漂很少的话(不可能为0,这不用我解释吧。。),那么只要改变\(x(t)\)的惩罚系数就行了啊~比如:
gains = LQRegulatorGains[
N[model], {DiagonalMatrix[{1000, 10, 10, 100}], {{1}}}] // First
有兴趣的可以自己去看看效果,基本就和你想象的差不多。。
然后原来的博文还做了一件丧心病狂的事情,就是突然增加一个冲击性的推力,比如说下面这个力,也就是说8秒的时候突然给一个力,然后16秒给一个更大的反向的力:
然后我们运行一下:
SimulatePendulum[controlforce + bumps[t]]
CDF演示
结果还是十分理想的,至少人来完成的话,基本可以上杂技节目了!!
写完收工
so~断断续续写了一周,总算写的差不多了,这篇就先这样吧,不知道有没有一开始不知道mathematica的同学突然对mathematica感兴趣起来了呢?仔细看下来的话,其实真的可以发现Mathematica在很多方面的运用是超级强大的!!
唉,有空吧后面的n节倒立摆稳定的给写完,因为事情有点多,而且虽然文章不长,但是写起来也略麻烦,虽然专门写了个函数来转gif,但是弄起来还是略麻烦。如果确定回来这里看的同学大部分都装了mathematica的话,那我下次就直接用cdf好了。。
关于下一篇,有兴趣的同学可以自己去先看原博客。
参考:
http://blog.wolfram.com/2011/01/19/stabilized-inverted-pendulum/
【完】
本文内容遵从CC版权协议,转载请注明出自http://www.kylen314.com

窝只懂物理…那个动能减势能是拉格朗日量的定义,如果我们定义一个函数叫x(t),还有它的导数x'(t),那么拉格朗日量就是这两个函数构成,它对时间积分得到作用量,这时候作用量与t无关了因为t被积分掉了,但是作用量可以看做是x这个函数的函数(其实就是泛函),我们不先验的知道这个x到底是个啥函数,任意的光滑函数都行,但是在众多函数之中只有一个函数复合真正的运动规律,那就是使得作用量变分为0的那个,这是最小作用量原理的准确描述。不过经典力学没有告诉我们为什么要是变分为0的那个才是符合物理的,但是量子力学有答案,因为量子力学是任意一个函数x,都对应有一个一个作用量S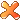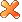 ,这个S当然不见得是最小的,但是量子力学是把所有的x按照”权重”求和得到粒子传播的概率振幅,这个权重就是exp(iS
,这个S当然不见得是最小的,但是量子力学是把所有的x按照”权重”求和得到粒子传播的概率振幅,这个权重就是exp(iS 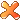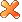 /hbar),hbar是约化普朗克常量,于是就会发现,求和之后只有S变分为0(经典路径)的附近的贡献是叠加的,越远离这个经典路径振荡越厉害,求和抵消了,所以最终的效果是只有经典路径附近概率最大。。。好像一下扯太远了
/hbar),hbar是约化普朗克常量,于是就会发现,求和之后只有S变分为0(经典路径)的附近的贡献是叠加的,越远离这个经典路径振荡越厉害,求和抵消了,所以最终的效果是只有经典路径附近概率最大。。。好像一下扯太远了
S[ x ]。。。怎么变成奇怪的字体了
多说留言是这样的,所以我们一般都是s【i】这么敲。。唉。。后面量子力学分析那个第一次听说。。。有点明白,但是又好像不怎么明白。。
1/2mv^2是动能吧
嗯,手滑,多谢指正。。其实这种远古博文平时没人看。。
如果要考虑边界条件应该怎么办?因为那个杆一旦倒在车上(认为杆和车完全非弹性碰撞使得相对速度为0)就不会再起来了啊
什么意思?杆的极限位置就是水平状态?
对,就比如第一次不施加外力的情况,gif中显示杆从水平面下转了回来,但是实际上这是不可能的,应该是杆一接触水平面就立刻静止才对
有一个问题啊,楼主,在计算L的时候,摆杆的势能里是不是少一个g(重力加速度)?